学习心得
| 名称 |
值 |
值 |
| X坐标 |
1 |
0 |
| Y坐标 |
0 |
1 |
| 偏移量 |
0 |
0 |
相当于 (0, 0), X (1, 0), Y (0, 1) 三个点决定了一个矩形
通过计算得到新的 X, Y , 然后再通过平移得到最终的坐标
平移
最简单, 修改平移值即可
| 名称 |
值 |
值 |
| X坐标 |
1 |
0 |
| Y坐标 |
0 |
1 |
| 偏移量 |
横向平移 |
纵向平移 |
缩放
在 x 轴与 y 轴上放大倍数
| 名称 |
值 |
值 |
| X坐标 |
X轴指定缩放倍数 |
0 |
| Y坐标 |
0 |
轴指定缩放倍数 |
| 偏移量 |
0 |
0 |
旋转
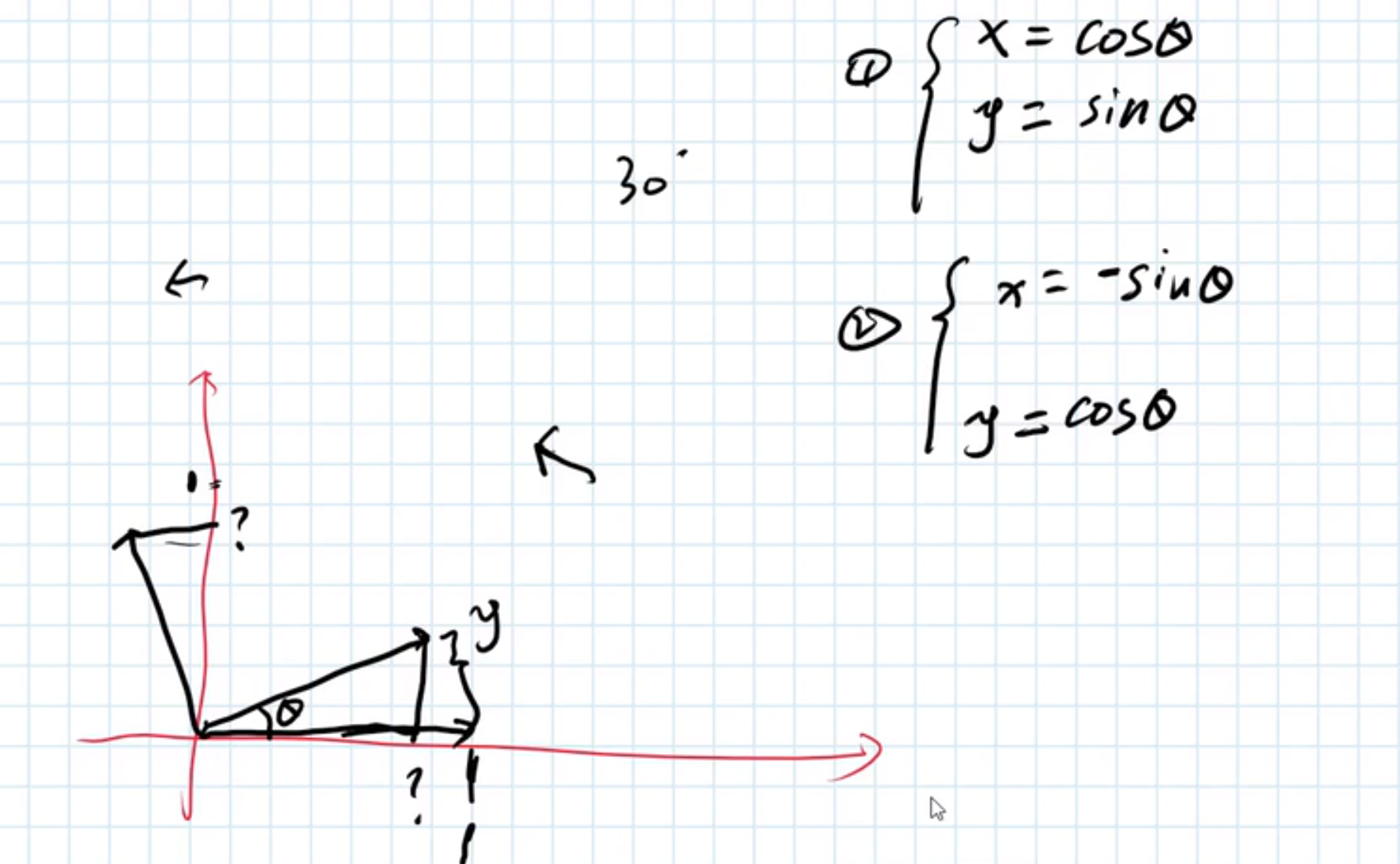
通过坐标旋转计算, 如果旋转角度为 θ
| 名称 |
值 |
值 |
| X坐标 |
cosθ |
sinθ |
| Y坐标 |
-sinθ |
cosθ |
| 偏移量 |
0 |
0 |
double angle = 45; // 旋转45度
double radians = angle * Math.PI / 180.0; # c# 使用弧度进行计算
double cos = Math.Cos(radians);
double sin = Math.Sin(radians);
Matrix rotateMatrix = new Matrix
{
M11 = cos,
M12 = sin,
M21 = -sin,
M22 = cos,
OffsetX = 0,
OffsetY = 0
};
倾斜
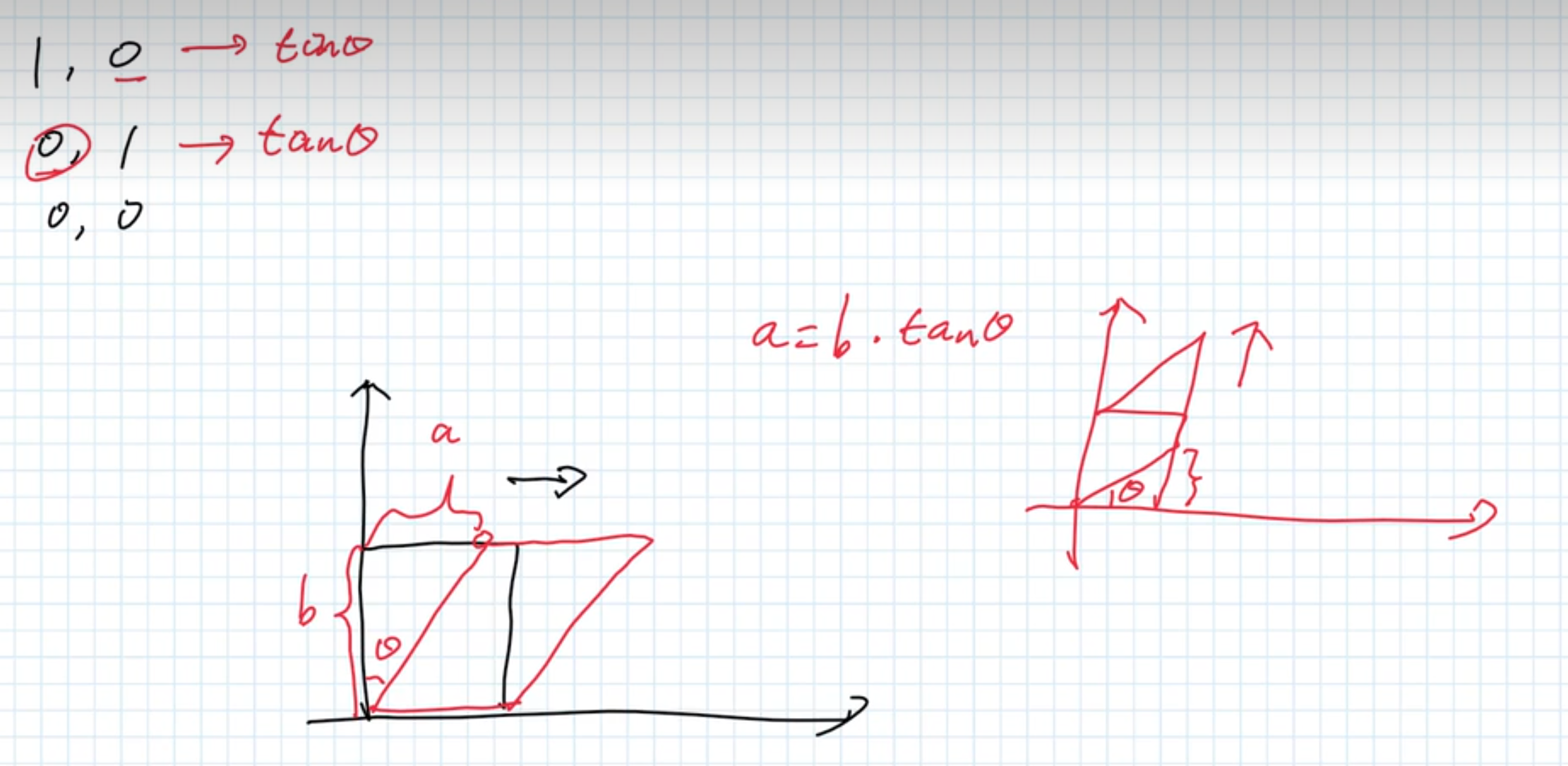
沿 X 方向倾斜 θ 度
| 名称 |
值 |
值 |
| X坐标 |
1 |
tanθ |
| Y坐标 |
0 |
1 |
| 偏移量 |
0 |
0 |
沿 Y 方向倾斜 φ 度
| 名称 |
值 |
值 |
| X坐标 |
1 |
0 |
| Y坐标 |
tanφ |
1 |
| 偏移量 |
0 |
0 |
计算例子
// 创建单位矩阵,即初始的矩阵
Matrix matrix = Matrix.Identity;
// 步骤1:缩放 - 放大 2 倍
matrix.Scale(2, 2);
// 步骤2:旋转 - 顺时针 45 度
matrix.Rotate(45);
// 步骤3:倾斜 - X 方向倾斜 30 度
matrix.Skew(30, 0);
// 步骤4:平移 - 移动到 (200, 100)
matrix.Translate(200, 100);
// 用来计算的初始点
Point point = new Point(100, 50);
// 应用变换, 得到转换后的点
Point transformedPoint = matrix.Transform(point);
Console.WriteLine($"变换后的坐标: ({transformedPoint.X:F2}, {transformedPoint.Y:F2})");
学习视频
WPF Matrix矩阵变 旋转 斜切,实用讲解,糖君哒
二维图形的坐标变换矩阵推导及齐次坐标, 有推导过程
俗说矩阵, 晓之车高山老师,有讲到齐次矩阵
其它一些资料
无所不能的矩阵 - 三维图形变换 https://www.bilibili.com/video/BV1b34y1y7nF
【线性代数】矩阵的运算 https://www.bilibili.com/video/BV1dm4y1q76a
无痛线代(6课) https://www.bilibili.com/video/BV1wu411T7dj
俗说矩阵(48课) https://www.bilibili.com/video/BV1aA411A7h3